Calculo de las coordenadas de los mojones

Calculo de área del terreno a partir de las coordenadas de los mojones. 

Se realiza el siguiente procedimiento.

• Ubicamos las coordenadas de los mojones para esto se calcula así: 

En el cálculo anterior de la poligonal se obtuvo los rumbos y coordenadas de los vértices del polígono y esto se tomara de base así: 

• Para el mojón 1 se tomara el rumbo del tramo de 5 – 1 en este caso es de n39°27’41.5”w y su respectiva distancia del p1 al m1 en este caso es de 16.25 mt y un ángulo de deflexión de -50°49’45.5”. 

• Con esta información se calcula el rumbo del punto 1 al mojón y sus respectivas proyecciones y luego poder obtener sus coordenadas . 

Para obtener las coordenadas de los mojones necesitamos:

Las distancias y los ángulos de deflexión de cada mojón así: 

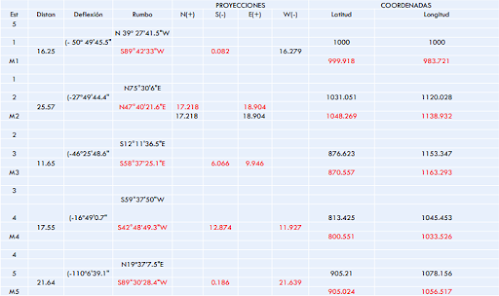
Hoja de coordenadas de los mojones.

Calculo del área del terreno a partir de los mojones.

1. Las proyecciones de los lados del lote, formado por los mojones

2. Los rumbos de los mojones del lote

3. Los ángulos de deflexión de cada mojón del lote

4. Las distancias de los lados del lote

5. Las dobles longitud

6. El área del lote o terreno cálculo de las proyecciones de los lados que delimiten el lote:

• PARA CALCULAR LAS PROYECCIONES NORTE O SUR. 

Utilizaremos las latitudes; observando que si entre dos mojones consecutivos, siguiendo el sentido del cadenamiento, aumenta el valor de la latitud, tenemos entonces una proyección positiva (norte), y si disminuye será proyección negativa (sur), con un valor igual a la diferencia entre ambas latitudes.

• PARA CALCULAR LAS PROYECCIONES ESTE U OESTE 

Utilizaremos las longitudes y procedemos de igual forma que para las proyecciones norte – sur; es decir, que si el valor de la longitud aumenta tenemos una proyección positiva (este), y negativa (oeste) si disminuye, con un valor igual a la diferencia entre las longitudes de los dos mojones consecutivos. 

Los rumbos de los mojones del terreno.

LOS RUMBOS DE LOS MOJONES DEL LOTE

• Para determinar los rumbos de los lados del lote utilizaremos las proyecciones calculadas siguiendo la siguiente metodología, EL ÁNGULO QUE DEFINIRÁ CADA LÍNEA SERÁ:

• ANGULO = T AN-1 (PROYECCIÓN ESTE- OESTE / PROYECCIÓN NORTE – SUR)

• RboM1-M2= Tan inv 155.211/48.351 =3.210088726 aplicamos inv tg y tenemos

• El cuadrante lo determinará el que las proyecciones sean NORTE, SUR, ESTE, OESTE. Como sus proyecciones son norte-este, entonces el rumbo de la línea M1-M2, será: N72°41’50.12”E 

Los ángulos de deflexion de cada mojon del terreno.

 Para calcular estos ángulos de deflexión, determinaremos los azimut de cada línea a partir de los rumbos obtenidos según el calculo anterior, la diferencia entre los azimut será el ángulo de deflexión en cada mojón del lote, siendo positivo si el azimut aumenta, y negativo si disminuye.

La diferencia es la deflexion pero se observa que el azimut aumenta su signo sera positivo + y si el azimut disminuye sera negativo - .

Las distancias de los lados del terreno y las dobles longitudes.

Las distancias las calculamos con la siguiente formula.

Distancia = √(proyección Norte-Sur)2 + (proyección Estre-Oeste)2

Cálculo de las Dobles Longitudes.

Para calcular las dobles longitudes observaremos las proyecciones Este-Oeste, y fijaremos como cantidad de partida la proyección positiva que sea suficiente para que no obtengamos dobles longitudes negativas, es decir, la proyección que se encuentre más al Este. (La longitud más el Este o sea aquella proyección que corresponde al menor valor en longitud). También fijaremos una cantidad de cierre, que será la proyección que se encuentra inmediatamente antes que la de partida, siguiendo el sentido del cadenamiento.

Bibliográfia.

• Ing. Raúl Bermúdez, Apuntes tomados de clase 

Cálculos de las coordenadas de la poligonal

 CALCULO DE LOS ÁNGULOS DE DEFLEXIÓN, CALCULO DE LOS RUMBOS Y SUS RESPECTIVAS PROYECCIONES. 

Calculo de poligonales cerradas.

En una poligonal cerrada es posible por medio de relaciones geométricas determinar el error angular de cierre.

Se puede determinar el error lineal de cierre debido a los errores angulares y de las distancias, comparando las coordenadas del punto inicial tal como originalmente se supuso y de las obtenidas por el calculo de los ángulos y distancias sucesivas a lo lardo de la poligonal.

1. En una poligonal cerrada existe una comprobación de cierre angular. Σ < 𝑑𝑒𝑓𝑙𝑒𝑥𝑖𝑜𝑛 = ±360
2. Existe un error permisible que es aquel error probable máximo que puede dar en una medida.  𝐸𝑝 = 𝑎√𝑛 
3. Cierre en distancia generalmente lo medimos por el cierre de precisión. 𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 ∶ 1 Σ𝑑𝑖𝑠𝑡 /𝑒𝑟𝑟𝑜r

En todo calculo de hojas de coordenadas se encuentran los errores en sus proyecciones:

• ERRORES EN SUS PROYECCIONES: 

• ERROR EN LATITUD : eN-S: ESTO ES 

• 𝐸𝑟𝑟𝑜𝑟 𝑙𝑎𝑡𝑖𝑡𝑢𝑑 = ∑ 𝑃𝑟𝑜𝑦. 𝑁 − ∑ 𝑃𝑟𝑜𝑦. 𝑆 

• ERROR EN LONGITUD : eE-W : 

• 𝐸𝑟𝑟𝑜𝑟 𝑙𝑜𝑛𝑔𝑖𝑡𝑢𝑑 = Σ𝑃𝑟𝑜𝑦. 𝐸 − Σ𝑝𝑟𝑜𝑦. 𝑊 

• ERROR TOTAL EN DISTANCIA SERÁ: 

• 𝐸𝑡𝑑 = √𝐸𝑑𝑙𝑎𝑡𝑖𝑡𝑢𝑑 2 + (𝐸𝑑𝐿𝑜𝑛𝑔𝑖𝑡𝑢𝑑) 2

Tabla y su división: 

Estación viene de campo Distancia viene de campo 

Las deflexiones viene de campo pero hay que hacer un ajuste 

Los rumbos se calculan a partir del azimut base y los ángulos de deflexión corregidos 

Las proyecciones a partir de las distancias y el rumbo y hay que aplicarle corrección para que cierren 

Las coordenadas a partir de las coordenadas si es latitud con el norte y sur y si es Longitud con Este y Oeste

Calculo de poligonales.

El procedimiento a seguir es el siguiente:

• Calculo de coordenadas del polígono base.
• Calculo de las coordenadas de los mojones del lote o terreno.
• Calculo del área del terreno 
• Calculo de coordenadas del polígono base.
• Calculo de los ángulos de deflexion.
• Calculo de los rumbos a partir de azimit de inicio de unos de sis tramos.
• Calculo de las proyecciones Norte-Sur y Este-Oeste.

Calculo de sus Rumbos 

Calculo de una hoja de coordenadas

• Con sus proyecciones y corrección.
• Calculo de las coordenadas latitud y longitud, corrección por la regla del transito y calculo de coordenadas de los  mojones.

Cálculos de las proyecciones.

• • Calculo de los ángulos de deflexión 
• • Calculo de los rumbos a partir de azimut de inicio de unos de sus tramos. 
• • Calculo de las proyecciones norte – sur ; y este – oeste 
• • para obtener estas proyecciones multiplicamos la longitud de cada lado por la función coseno y seno del rumbo de cada lado. 
• • latitud distancia x coseno del rumbo = norte (+) o sur (-) 
• • longitud distancia x seno del rumbo = este (+) o oeste (-) 

Representación para uso de calculadora.

SHIFT REC REC(DIST,RUMBO)= LA PRIMER PROYECCION N o S LUEGO ALFA F RCL = LA SEGUNDA PROY. E o W.

Tabulando los datos de las deflexiones, rumbos, proyecciones y coordenadas.

Bibliográfia.

• Ing. Raúl Bermúdez, Apuntes tomados de clase 

El Teodolito.

 El Teodolito o Transito.

El teodolito es un instrumento de medición mecánico-óptico que se utiliza para obtener ángulos verticales y horizontales, en la mayoría de los casos, ámbito en el cual tiene una precisión elevada. 

Con otras herramientas auxiliares puede medir distancias y desniveles. 

Es portátil y manual; está hecho con fines topográficos e ingenieriles, sobre todo para las triangulaciones. Con ayuda de una mira y mediante la taquimetria, puede medir distancias. 

Un equipo más moderno y sofisticado es el teodolito electrónico, y otro instrumento más sofisticado es otro tipo de teodolito más conocido como estación total.

Básicamente, el teodolito actual es un telescopio montado sobre un trípode y con dos círculos graduados, uno vertical y otro horizontal, con los que se miden los ángulos con ayuda de lentes.

El teodolito también es una herramienta muy sencilla de transportar. Por eso es una herramienta que tiene muchas garantías y ventajas en su utilización. Es su precisión en el campo lo que lo hace importante y necesario para la construcción.

Partes del teodolito

Niveles: Este es un tubo pequeño cerrado que tiene una mezcla de eter y alcohol junto a una burbuja de aire, la tangente a esta es un plano horizontal. Puede trabajarse con los niveles descorregidos,

Precisión: Esta dependerá de la clase de teodolito que se use. Están los antiguos que tienen una variación entre el minuto y el  minuto y medio; y los modernos  que cuentan con una precisión de entre 10, 6, 1 y 0.1.

Nivel esférico: Esta es una caja tapada y cilíndrica a través de un casquete esférico. mientras menor sea el radio de curvatura, menos sensibilidad tendrán, se utilizan para conseguir de manera rápida el plano horizontal. en el centro poseen un circulo donde se coloca la brújula a fin de encontrar un plano horizontal que se le aproxime. tienen menor precisión que los niveles tóricos, su nivel esta en 1 como máximo y lo normal es 10 o 12.

Nivel tórico: Se utiliza para establecer la orientación al aparato y saber las direcciones medidas de acuerdo al norte, en caso de conocer el acimutal.

Plomada: Es usada a fin de que el teodolito se posicione en la misma vertical en la que está el punto del suelo.

Plomada de gravedad: Su manejo es muy incomodo y termina siendo un poco precisa en los días de viento. este tipo de método se usaba antes de que se implementara la plomada óptica. 

Plomada óptica: Esta integrada actualmente en los teodolitos, el suelo puede visualizarse a través del ocular y se coloca el aparato en  la misma vertical que el punto de búsqueda.

Limbos:  Estos son discos graduados que posibilitan hallar los ángulos. se divide de 0 a 360 grados sexagesimales como también de 0 a 400 grados centesimales. 

Nonius: Es una herramienta que posibilita disminuir o aumentar la precisión del limbo.

Micrómetro: Mecanismo óptico que posibilita realizar la función de los nonios pero permitiendo observar un rayo optico y una serie de graduaciones a travez de mecanismo que aumentaran la precisión.

Tripodes: Se usan para un mejor trabajo, poseen la misma Y e X pero una Z distinta, tienen una altura y el que mas se utiliza es el de la maseta.

Tornillo de presión: Este tornillo esta señalizado en color amarillo, se usa para fijar el movimiento particular de los indices y tiene la capacidad de desplazar el disco negro solidario a través del aparato. 

Tornillo de coincidencia: Mecanismo que permite mover el aparato hasta que coincida la linea vertical de la cruz filar con la vertical buscada.

Centrado del teodolito

En el centrado del teodolito es colocar e aparato en una de las estaciones el cual tiene un trompo con clavo el cual el aparato se ubica sobre el. 

Usos del teodolito

Simples: Valiéndose del botón del movimiento general 

Por repetición: Tiene por objeto obtener el valor de un angulo lo mas próximo posible a su valor verdadero que puede dar directamente las instrucciones debido a su escasa aproximación < 𝐴 = 𝐿𝑒𝑐𝑡𝑢𝑟𝑎 𝑓𝑖𝑛𝑎𝑙 − 𝑙𝑒𝑐𝑡𝑢𝑟𝑎 𝑖𝑛𝑖𝑐𝑖𝑎𝑙 ÷ # 𝑑𝑒 𝑟𝑒𝑝𝑒𝑡𝑖𝑐𝑖𝑜𝑛𝑒

Medición por angulo de deflexión 

• DEFLEXION: es el Angulo formado en un vértice de la poligonal por la prolongación del lado anterior con el lado siguiente.- 

Dependiendo del sentido en que se obtenga el ángulo de la deflexión será: 

• DERECHA O POSITIVA(+) en el sentido horario 

• IZQUIERDA O NEGATIVA(-) : en el sentido anti horario.

COMO SE OBTIENEN LAS DEFLEXIONES: 

• En cada vértice se ve el punto de atrás , se da una vuelta de campana y se gira el anteojo para ver el punto adelante.

Formas de anotar en la libreta 

Cuando se realiza un levantamiento topográfico la forma de anotar en la libreta es la siguiente: 

Bibliográfia.

• Ing. Raúl Bermúdez, Apuntes tomados de clase