Tipo de escalas, levantamientos con cinta de un terreno.

Escala 

La escala es la relación de proporción entre las dimensiones reales de un objeto y las del dibujo que lo representa. Ejemplo: si una escala indica una proporción 1:15000 significa que un centímetro del mapa representa 15000 en la vida real.

• La escala numérica representa la relación entre el valor de la representación (el número a la izquierda del símbolo ":") y el valor de la realidad (el número a la derecha del símbolo ":") y un ejemplo de ello sería 1:100 000, lo que indica que una unidad cualquiera en el plano representa 100 000 de esas mismas unidades en realidad, dicho de otro modo, dos puntos que en el plano se encuentran a 1 cm y estarán en la realidad a 100 000 cm, si están en el plano a 1 m en la realidad estarán a 100 000 metros, y así con cualquier unidad que tomemos.

• La escala unidad por unidad es la igualdad expresa de dos longitudes: la del mapa (a la izquierda del signo "=") y la de la realidad (a la derecha del signo "="). Un ejemplo de ello sería 1 cm = 4 km; 2 cm = 500 m, etc.

• La escala gráfica es la representación dibujada de la escala unidad por unidad, donde cada segmento muestra la relación entre la longitud de la representación y el de la realidad. Un ejemplo de ello sería: 1 cm__o__10 km

Fórmula: N=P/T​
Donde: 

N: Escala; 

P: Dimensiones en el papel (cm, m); 

T: Dimensiones en el terreno (cm, m); ambos deben estar en una misma unidad de medida.

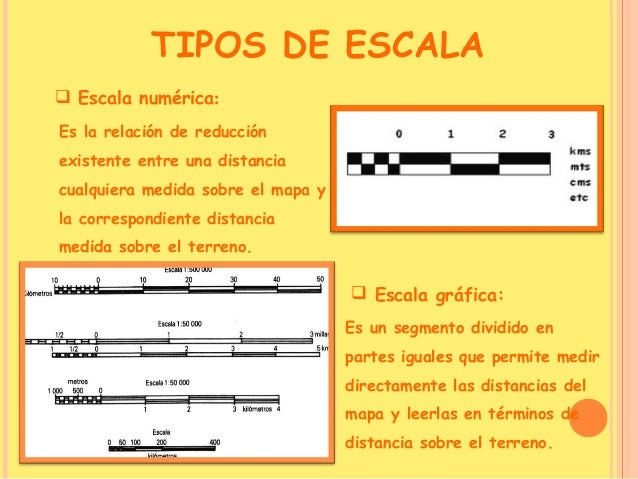
Tipos de escalas.

Existen tres tipos de escalas:

• Escala natural: Es cuando el tamaño físico del objeto representado en el plano coincide con la realidad. Existen varios formatos normalizados de planos para procurar ocupar espacios de reducción.

• Escala de reducción: Se utiliza cuando el tamaño físico del plano es menor que la realidad. Esta escala se utiliza para representar piezas (E.1:2 o E.1:5), planos de viviendas (E:1:50), mapas físicos de territorios donde la reducción es mucho mayor y pueden ser escalas del orden de E.1:50.000 o E.1:100.000. Para conocer el valor real de una dimensión hay que multiplicar la medida del plano por el valor del denominador.

• Escala de ampliación: Se utiliza cuando hay que hacer el plano de piezas muy pequeñas o de detalles de un plano. En este caso el valor del numerador es más alto que el valor del denominador o sea que se deberá dividir por el numerador para conocer el valor real de la pieza.

Clases de cinta. 

Una cinta métrica es la reproducción de un numero determinado de veces (3,5,30,50,100) de la unidad patrón.

las cintas son sometidas a diferentes tensiones y temperaturas, por lo que dependiendo del material con el que a sido construidas.su tamaño original variara.

por esta razón, las cintas vienen calibradas de fabrica para que a una temperatura o tensión y condiciones de apoyo dadas, su longitud sea igual a la longitud nominal.

las cintas métricas empleadas en trabajos topográficos deben ser de acero, resistentes a esfuerzos de tensión y a la corrosión, comúnmente, las cintas métricas vienen en longitudes de 30,50, 100 m,  con una sección transversal de 8 mm x 0,45 mm para trabajos fuertes en condiciones severas o de 6 mm x 0,30 mm para trabajos en condiciones normales.

Recomendaciones para el uso de la cinta

• Verificar el estado de la cinta antes de comenzar a medir 
• Tener la seguridad de que la cinta enrolle con facilidad
• Que tenga los números visibles 
• Después de usar la cinta verificar que se encuentre limpia para poder guardarla

Errores en la medición con cinta

Precisión en la medición con cinta.

si la medición se efectúa sin ampliar la tensión suficiente no son muy experto en mantener cadeneros no son muy expertos en mantener dentro de ciertos limites razonables, la horizontalidad de la cinta, la precisión de ser baja.

Algunos errores que se pueden tener a la hora de medir con la cinta. 

Los errores sistemáticos son aquellos que pueden ser eliminados o atenuados aplicando alguna teoría física o expresión matemática que los defina. 

•  Error de pendiente: Cuando se toma la distancia geométrica, en vez de la distancia reducida. 
•  Error de graduación por falta de contraste: Se debe a la incorrecta longitud de la cinta, por lo que no debe medirse con una cinta sin conocer su longitud contrastada, sobre todo si ha sufrido roturas y reparaciones.
• Error por falta de alineación: cuando el delantero no está bien alineado, al clavar la ficha lo hace fuera de alineación, cometiendo un error acumulativo, siendo en todos los casos la longitud real menor que la medida tomada (error positivo). 
• Error por catenaria: cuando la cinta no está apoyada sobre el terreno sino suspendida de sus extremos adopta la forma de catenaria, originando un error que como el anterior es acumulativo siendo la longitud real menor que la medida. Este error es más característico en las mediciones geodésicas y poco frecuentes en Topografía.
• Error por temperatura: cuando la cinta es utilizada a temperaturas mayores o menores a las de calibración de fabrica, debido a esta variación de temperatura la cinta se contrae o dilata generando un cambio en la longitud de la misma.
• entre otros.

                    

                    

Levantamiento de un terreno con cinta 

Cuando se va a levantar un terreno relativamente pequeño se puede hacer con cinta, llevando el proceso de subdividir el área dada en figuras como triángulos, rectángulos etc. 

Al principio se tiene que hacer un reconocimiento de todo el terreno 

Existen diversos factores para poder tener una mejor elección en el terreno.

• Seleccionar adecuadamente los lados del polígono 
• Distribución de triángulos bien conformados 
• Estabilidad y permanencia de las estaciones o mojones
• Estaciones bien referenciadas
• Visibilidad entre estaciones 

Polígono de base triangular 

Procedimiento: 

• Reconocimiento.
• Trazo y medición del polígono base, incluyendo diagonales.
• Levantamiento de detalles con relación al polígono.
• Dibujo de lo levantado
• Calculo del área total.

Ángulos de un triangulo

 Método de lados de liga

En este método es utilizado cuando el terreno es encerrado por un polígono y es de tal naturaleza que no permite el empleo de los métodos anteriores porque existen obstáculos que impiden ver tres vértices consecutivos del polígono base.

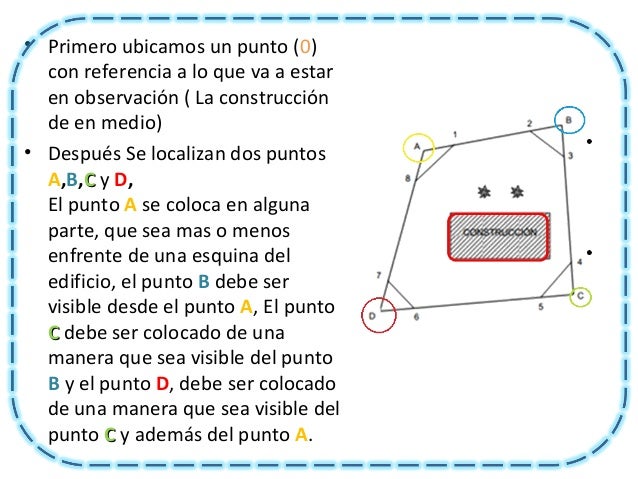
Procedimiento para lado de liga 

Métodos de lado de liga: se mide a, b, c, en cada vértice; donde b es el lado de la liga y el angulo se calcula . 

                   angulo  = 2 arc sen* s/ 2 a

En cada vértice se realizan las distancias atrás y otra adelante que sean iguales 

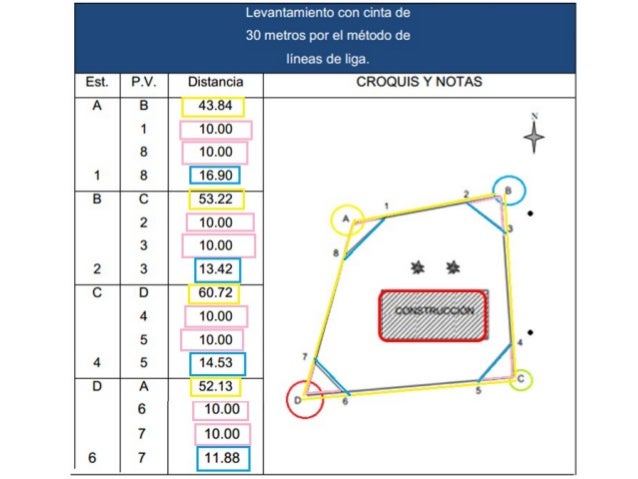
Comprobación de los ángulos 

• Internos es igual a 180 (n-2), los 
• Ángulos externos  es igual 180 (n+2) 

 en donde n es el numero de vértices del polígono 

tolerancia angular = 0.5º √n

Bibliográfia.

• Ing. Raúl Bermúdez, Apuntes tomados de clase